Методическая разработка ключевой задачи
 Задача 2.
Задача 2.
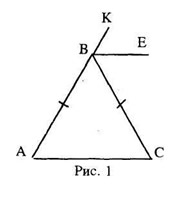
Пусть дан равнобедренный треугольник ABC (AB=BC). Доказать, что биссектриса внешнего угла треугольника параллельна основанию (Рис. 1).
При выполнении можно действовать различными способами.
Рассмотрим некоторые из них.
1. Можно получать следствия из условия, для этого имеет смысл:
 - изучить объекты, которые фигурируют в задаче и применить известные свойства этих объектов;
- изучить объекты, которые фигурируют в задаче и применить известные свойства этих объектов;
- попытаться совместить свойства разных объектов, которые фигурируют в задаче;
- применить известные утверждения;
- высказать и доказать какое-то предположение.
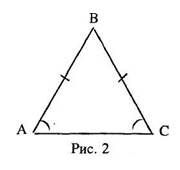
Изучая объекты, фигурирующие в задаче, имеет смысл обратиться к треугольнику ABC. Известно, что в равнобедренном треугольнике углы при основании равны, поэтому из условия задачи получаем следствие: ∠А=∠C (Рис. 2).
 Можно и далее, опираясь на известные свойства равнобедренного треугольника, получать новые следствия (советуем попытаться это сделать).
Можно и далее, опираясь на известные свойства равнобедренного треугольника, получать новые следствия (советуем попытаться это сделать).
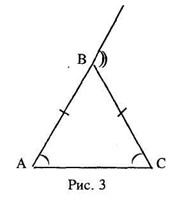
Обратимся к другому объекту - внешний угол КВС треугольника ABC (Рис. 3). Опираясь на доказанное свойство внешнего угла, получаем новое следствие: ∠KBC=∠A+∠C.
Теперь, опираясь на полученные следствия,
получаем: ∠EBC= 1/2 ∠KBC= 1/2(∠A+∠C)= 2∙1/2 ∠C=∠C.
Так как углы ЕВС и С внутренние накрест лежащие углы при прямых BE, АС и секущей ВС - равны, то прямые BE и АС - параллельны. Утверждение доказано.
2. При поиске метода решения задач помогают связи с тем, что встречалось ранее. Покажем, каким образом могут быть использованы такие связи. (Обратите внимание на то, как выявляется и используется связь при поиске метода решения).
Прежде всего выясним, что представлено на? (Рис.4)
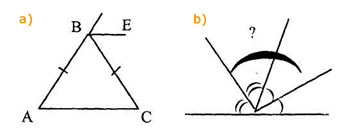
Имеются смежные углы.
1. Проведены биссектрисы смежных углов.
2. Предлагается вспомнить, какой угол образуют между собой биссектрисы смежных углов.
Найдя ответ в учебнике, вспомнив его или доказав в данный момент, приходим к выводу: Биссектрисы смежных углов перпендикулярны.
Неизвестно, все ли прочитали на рис.5 (возможно, если не удастся найти решение, то придется вернуться к рис. 5 и попытаться «увидеть» новые факты), но можно обратиться к поиску ответа на вопросы, как использовать то, что удалось установить по рис.5. Для этого следует рисунок 4а сопоставить с тем, что узнали, и дополнить его таким образом, чтобы удалось использовать выявленные факты.
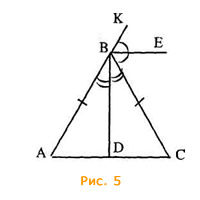
Имеется биссектриса угла KBС. Ему смежен угол ABC. Для этого угла нет биссектрисы, поэтому, чтобы воспользоваться (Рис.4b), следует провести биссектрису BD угла ABC (Рис.5).
Из предыдущего получаем ∠DBE=90°.
Теперь, чтобы убедиться в параллельности BE и АС, достаточно доказать, что BD перпендикулярна AC. Это легко сделать, опираясь на свойство биссектрисы равнобедренного треугольника - она являются медианой и высотой. Таким образом, вновь получаем справедливость доказываемого утверждения.
3. Полезно помнить и систематизировать некоторые эвристики (соображения или действия, которые могут в случае применяемости быстро получить требуемые результаты,
 хотя и не гарантируют его получения). В предыдущим решении эвристика состояла в том, что имеется часть знакомой ситуации и в таком случае требуется уменьшить отличия в ситуациях, выполнив дополнительное построение.
хотя и не гарантируют его получения). В предыдущим решении эвристика состояла в том, что имеется часть знакомой ситуации и в таком случае требуется уменьшить отличия в ситуациях, выполнив дополнительное построение.Вот одна еще одна полезная эвристика: если имеются равные отрезки, то имеет смысл дополнительно отложить новый отрезок (или отрезки), равный данному.
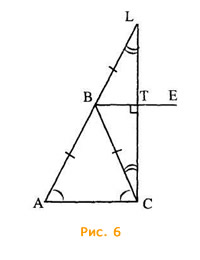
Стремясь использовать эту эвристику на луче АВ, за точку В, отложим BL=AB=BC (Рис. 6) и L соединим с С. В результате выполненных действий получились новые объекты, поэтому важно выполнить наблюдение и получить новые следствия.
На первом шаге наблюдения стараемся "заметить", как можно больше объектов, которые имеются на рисунке. Здесь можно "заметить: ΔАВС, ΔBLC, ΔALC, четырехугольник АВТС, ABLT, LCT и др.
Теперь пользуясь известными фактами и свойствами объектов, получаем следствия:
ΔАВС: ∠A=∠C;
ΔBLC: ∠BLC=∠BCL, BT⊥LC;
ΔALC: ∠ACL=∠LAC+ ∠ALC=90°.
Далее можно не получать новые следствия, так как из того, что BT⊥LC и AC⊥LC получаем, что BE || AC, т.е. вновь обосновано доказываемое утверждение.
4. Часто, чтобы доказать какое-либо утверждение, поступают следующим образом:
 1. Строят объект с требуемыми свойствами.
1. Строят объект с требуемыми свойствами.2. Доказывают, что построенный объект совпадает с тем, который был дан в условии.
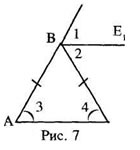
Пытаясь реализовать эту идею, проведем прямую ВЕ1 || AС (Рис.7).
Так как BE1 || AC, то ∠1=∠3 (Почему?) и ∠2=∠4 (Почему?). Известно, что ∠3=∠4, поэтому ∠1=∠2. Следовательно, BE является биссектрисой внешнего угла КВС. Этот метод иногда называют «начни с конца».
5. Достаточно часто при доказательстве утверждений пользуют¬ся методом, который называется «методом от противного». Реализация этого метода сводится к таким шагам:
1. Предполагается, что доказываемое утверждение неверно.
2. Опираясь на предположение и условия, с помощью тех или иных рассуждений получают противоречие (либо с некоторым предположением, либо с условием, либо с доказанным ранее утверждением).
Попытайтесь самостоятельно доказать параллельность BE и АС методом от противного.
Дополнительно рекомендуется: попытаться сформулировать и проверить истинность обратной задачи, попытаться обобщить исходную задачу.
Перейти к условию задачи
Вернуться к теме занятия
Задача 4.
Внутри квадрата АВСД проведены прямые через вершины А и Д так, что они образуют со стороной АД углы в 15°. Пусть Е – точка пересечения прямых. Докажите, что треугольник ВЕС равносторонний.
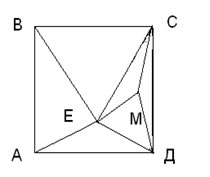 Решение. Построим равносторонний треугольник ЕМД и точку М соединим с вершиной С.
Решение. Построим равносторонний треугольник ЕМД и точку М соединим с вершиной С.
1. Докажем, что треугольники АЕД и ДМС равны. Действительно, АД=СД – это стороны квадрата АВСД.
ДЕ=ДМ – по построению. Легко убедиться, что ∠АДЕ=∠СДМ=15°.
Треугольники равны по первому признаку равенства треугольников.
Из равенства треугольников получаем: ∠ДСМ=∠АДЕ=15° и ∠СМД=150°.
2. Докажем, что треугольники СДМ и СЕМ равны. Действительно: ЕМ=ДМ – стороны равностороннего треугольника ЕМД. СМ – общая сторона треугольников.
Легко убедиться, что ∠СМД=∠СМЕ=150°.
Из равенства треугольников следует, что СЕ=СД. Аналогично доказывается, что ВЕ=АВ.
Утверждение доказано.
Метод, который использован при решении этой задачи, назовем методом вспомогательного равностороннего треугольника. Его применение основано на том, что после построения появляются новые равные элементы, что позволяет доказать и применить равенство треугольников. Его реализация осуществляется по такой схеме:
• Изучаются объекты, которые фигурируют в ситуации задачи;
• Выбирается объект, с участием которого строится равносторонний треугольник;
• Анализируется новая ситуация и получаются следствия для получения нужного результата.
